信号处理:指数移动平均 (EMA) 滤波器
之前我们在《信号处理简介》一文中已经见过了两类滤波器:有限脉冲响应 (FIR) 滤波器和无限脉冲响应 (IIR) 滤波器。我们看到了移动平均滤波器如何同时以 FIR 和 IIR 形式表示,但如果它们相互比较又各具哪些优势呢?
回顾我之前博客中的例子,我们可以将 FIR 滤波器展开为如下形式:
y[5] = (x[5]+x[4]+x[3]+x[2]+x[1]+x[0])/5,
在这里,我们看到我们需要:
- 5 次乘法和
- 4 次求和运算。
乘法运算的计算成本特别高。因此,如果我们再次查看 IIR 形式,我们会发现它只需要:
- 3 次乘法和
- 2 次求和运算
y[6]=(x[6]+y[5]-x[1])/5
这大大降低了计算成本!这对于单片机等嵌入式设备来说非常好,因为它们在每个离散时间步骤上执行计算所消耗的资源更少。
例如,当我对采用 FIR 和 IIR 形式的 11 点移动平均滤波器使用 Python 函数 ‘time.time’ 时,所有参数(窗口大小、采样率、样本大小等)相同,我分别得到以下运行时间结果:51 ms、27 ms。
离散时间 IIR 滤波器示例
现在我们已经了解了为什么 IIR 滤波器在单片机上表现更好了,让我们看一个使用 Arduino UNO 和 DFRobot MPU6050 惯性测量单元 (IMU) 的示例项目(图 1)。我们将对 IMU 数据应用指数移动平均 (EMA) 滤波器,以查看原始数据和平滑数据之间的差异。
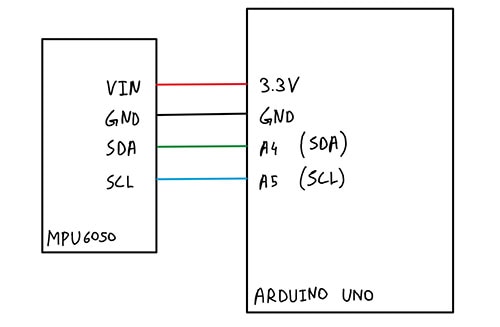 图 1:MPU6050 与 Arduino Uno 之间的连接框图。(图片来源:Mustahsin Zarif)
图 1:MPU6050 与 Arduino Uno 之间的连接框图。(图片来源:Mustahsin Zarif)
 图 2:MPU6050 与 Arduino Uno 之间的连接。(图片来源:Mustahsin Zarif)
图 2:MPU6050 与 Arduino Uno 之间的连接。(图片来源:Mustahsin Zarif)
指数移动平均滤波器具有递归形式:
y[n] = α*x[n] + (1- α)*y[n-1]
它之所以是递归,是因为我们测量的任何当前输出也取决于先前的输出;即系统具有记忆。
常数 alpha () 决定了我们想要赋予当前输入相对于先前输出多大的权重。为了清楚起见,让我们展开方程得到:
y[n] = α*x[n] + (1- α )*(α*x[n−1]+(1−α)*y[n−2])
y[n] = α*x[n] + (1- α )*x[n−1]+α*(1−α)2*x[n−2])+ ...
y[n] = k=0nα*(1−α)k*x[n−k]
我们看到,alpha 越大,当前输入对当前输出的影响就越大。这是好事,因为如果系统在不断演进,过去的值不能代表当前的系统。另一方面,如果系统突然发生瞬间异常变化,情况就会变得很糟糕;在这种情况下,我们希望我们的输出能够遵循之前输出所遵循的趋势。
事不宜迟,现在让我们看看 EMA 滤波器的代码是如何用于 MPU6050 的。
EMA 滤波器代码:
副本#include <wire.h>
#include <mpu6050.h>
MPU6050 mpu;
#define BUFFER_SIZE 11 // Window size
float accelXBuffer[BUFFER_SIZE];
float accelYBuffer[BUFFER_SIZE];
float accelZBuffer[BUFFER_SIZE];
int bufferCount = 0;
void setup() {
Serial.begin(115200);
Wire.begin();
mpu.initialize();
if (!mpu.testConnection()) {
Serial.println("MPU6050 connection failed!");
while (1);
}
int16_t ax, ay, az;
for (int i = 0; i < BUFFER_SIZE; i++) {
mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);
accelXBuffer[i] = ax / 16384.0;
accelYBuffer[i] = ay / 16384.0;
accelZBuffer[i] = az / 16384.0;
}
bufferCount = BUFFER_SIZE;
}
void loop() {
int16_t accelX, accelY, accelZ;
mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);
float accelX_float = accelX / 16384.0;
float accelY_float = accelY / 16384.0;
float accelZ_float = accelZ / 16384.0;
if (bufferCount < BUFFER_SIZE) {
accelXBuffer[bufferCount] = accelX_float;
accelYBuffer[bufferCount] = accelY_float;
accelZBuffer[bufferCount] = accelZ_float;
bufferCount++;
} else {
for (int i = 1; i < BUFFER_SIZE; i++) {
accelXBuffer[i - 1] = accelXBuffer[i];
accelYBuffer[i - 1] = accelYBuffer[i];
accelZBuffer[i - 1] = accelZBuffer[i];
}
accelXBuffer[BUFFER_SIZE - 1] = accelX_float;
accelYBuffer[BUFFER_SIZE - 1] = accelY_float;
accelZBuffer[BUFFER_SIZE - 1] = accelZ_float;
}
//calculate EMA using acceleration values stored in buffer
float emaAccelX = accelXBuffer[0];
float emaAccelY = accelYBuffer[0];
float emaAccelZ = accelZBuffer[0];
float alpha = 0.2;
for (int i = 1; i < bufferCount; i++) {
emaAccelX = alpha * accelXBuffer[i] + (1 - alpha) * emaAccelX;
emaAccelY = alpha * accelYBuffer[i] + (1 - alpha) * emaAccelY;
emaAccelZ = alpha * accelZBuffer[i] + (1 - alpha) * emaAccelZ;
}
Serial.print(accelX_float); Serial.print(",");
Serial.print(accelY_float); Serial.print(",");
Serial.print(accelZ_float); Serial.print(",");
Serial.print(emaAccelX); Serial.print(",");
Serial.print(emaAccelY); Serial.print(",");
Serial.println(emaAccelZ);
delay(100);
}
</mpu6050.h></wire.h>
当我们运行此代码并检查串口绘图仪时,我们可以看到 x、y 和 z 轴方向加速度的成对粗糙和平滑线条,其中窗口大小为 11 和 alpha 值为 0.2(图 3 至 5)。
 图 3:x 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
图 3:x 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
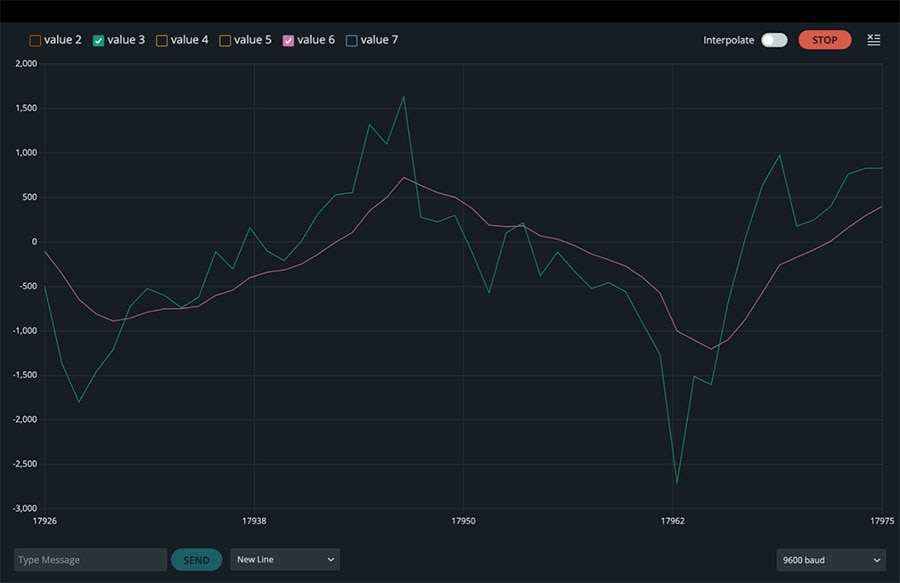 图 4:y 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
图 4:y 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
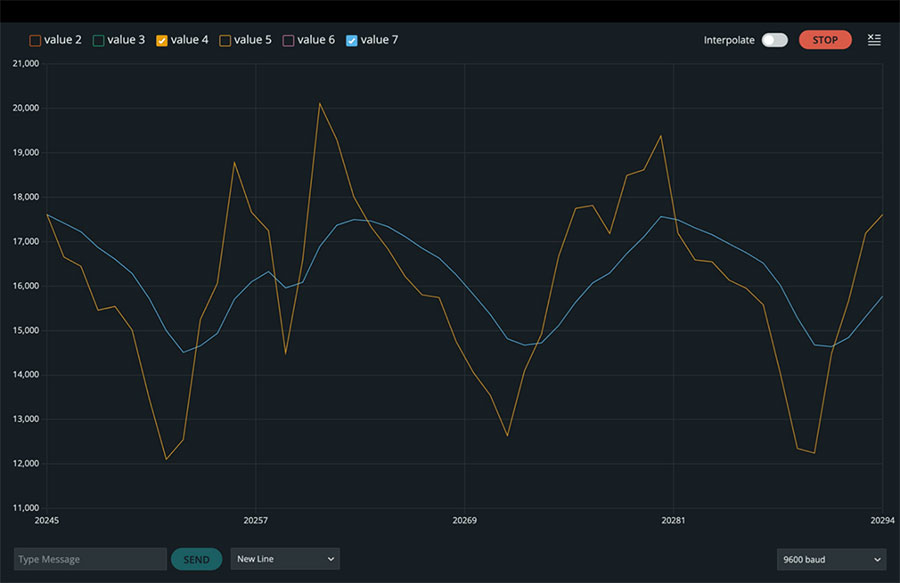 图 5:z 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
图 5:z 方向的原始加速度值和滤波后的加速度值。(图片来源:Mustahsin Zarif)
让代码的智能化更进一步
我们现在知道,与 FIR 滤波器相比,IIR 滤波器更适合用作控制器,因为所需的求和和乘法计算明显较少。然而,当我们实现这段代码时,执行的计算并不只有求和和乘法:每当有新的时间样本进入时,我们都必须移动样本,而这个过程在后台需要计算能力。因此,我们可以借助循环缓冲区,而不是在每个采样时间间隔移动所有样本。
我们的做法是:用一个指针来记住传入的数据样本的索引。然后,每次指针指向缓冲区中的最后一个元素时,它接下来都会指向缓冲区的第一个元素,新数据将替换之前存储在这里的数据,因为这是现在我们不再需要的最旧数据(图 6)。因此,这种方法允许我们跟踪缓冲区中最旧的样本并替换该样本,而不必每次都移动样本以将新数据放入数组的最后一个元素中。
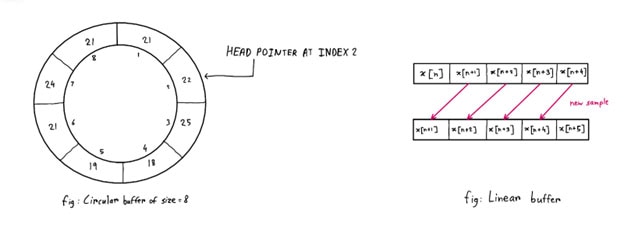 图 6:循环缓冲区示例图。(图片来源:Mustasin Zafir)
图 6:循环缓冲区示例图。(图片来源:Mustasin Zafir)
这是使用循环缓冲区的 EMA 滤波器实现的代码。您能尝试对陀螺仪而不是对加速计运行这段代码吗?也可以尝试使用不同的系数!
使用循环缓冲区代码的 EMA 滤波器:
副本#include <wire.h>
#include <mpu6050.h>
MPU6050 mpu;
#define BUFFER_SIZE 11 // Window size
float accelXBuffer[BUFFER_SIZE];
float accelYBuffer[BUFFER_SIZE];
float accelZBuffer[BUFFER_SIZE];
int bufferIndex = 0;
void setup() {
Serial.begin(115200);
Wire.begin();
mpu.initialize();
if (!mpu.testConnection()) {
Serial.println("MPU6050 connection failed!");
while (1);
}
int16_t ax, ay, az;
for (int i = 0; i < BUFFER_SIZE; i++) {
mpu.getMotion6(&ax, &ay, &az, NULL, NULL, NULL);
accelXBuffer[i] = ax / 16384.0;
accelYBuffer[i] = ay / 16384.0;
accelZBuffer[i] = az / 16384.0;
}
}
void loop() {
int16_t accelX, accelY, accelZ;
mpu.getMotion6(&accelX, &accelY, &accelZ, NULL, NULL, NULL);
float accelX_float = accelX / 16384.0;
float accelY_float = accelY / 16384.0;
float accelZ_float = accelZ / 16384.0;
accelXBuffer[bufferIndex] = accelX_float;
accelYBuffer[bufferIndex] = accelY_float;
accelZBuffer[bufferIndex] = accelZ_float;
bufferIndex = (bufferIndex + 1) % BUFFER_SIZE; //circular buffer implementation
float emaAccelX = accelXBuffer[bufferIndex];
float emaAccelY = accelYBuffer[bufferIndex];
float emaAccelZ = accelZBuffer[bufferIndex];
float alpha = 0.2;
for (int i = 1; i < BUFFER_SIZE; i++) {
int index = (bufferIndex + i) % BUFFER_SIZE;
emaAccelX = alpha accelXBuffer[index] + (1 - alpha) emaAccelX;
emaAccelY = alpha accelYBuffer[index] + (1 - alpha) emaAccelY;
emaAccelZ = alpha accelZBuffer[index] + (1 - alpha) emaAccelZ;
}
Serial.print(accelX_float); Serial.print(",");
Serial.print(emaAccelX); Serial.print(",");
Serial.print(accelY_float); Serial.print(",");
Serial.print(emaAccelY); Serial.print(",");
Serial.print(accelZ_float); Serial.print(",");
Serial.println(emaAccelZ);
delay(100);
}
</mpu6050.h></wire.h>
结语
在这篇博客中,我们讨论了 IIR 和 FIR 滤波器之间的区别,重点讨论了它们的计算效率。通过从 FIR 到 IIR 所需运算次数减少这一小例子,我们可以想象当应用规模化时 IIR 滤波器的效率会有多高,这对于硬件能力有限的实时应用非常重要。
我们还研究了一个使用 Arduino Uno 和 MPU6050 IMU 的示例项目,其中我们部署了一个指数移动平均滤波器来降低传感器数据中的噪声,同时仍然捕捉底层信号行为。最后,为了提高效率,我们提供了一个更智能的示例代码,即采用循环缓冲区而不是在每个时间间隔移动数据。
在下一篇博客中,我们将利用 Red Pitaya 的 FPGA 功能来实现一个 4 抽头 FIR 滤波器数字电路!

Have questions or comments? Continue the conversation on TechForum, Digi-Key's online community and technical resource.
Visit TechForum






