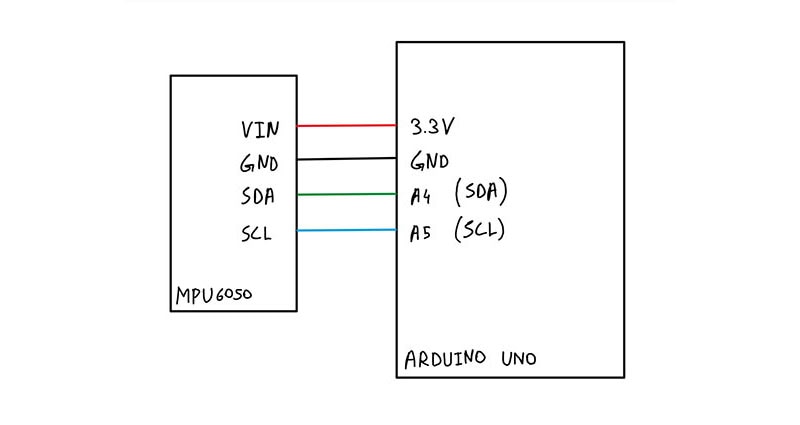
信号处理简介:移动平均滤波器
信号和系统是电气工程的核心概念。利用这两个概念,我们能够模拟信息是如何通过电气元件并被修改的。而且,一旦了解了不同的电气元件如何影响电压等信号,我们就可以设计电路,以任何我们想要的方式控制信号。我们竟然能够使用电阻器、电容器和运算放大器 (op-amps) 等电子元器件组合来模拟积分和微分等数学工具,这着实令人惊叹。
例如以下电路(图1):
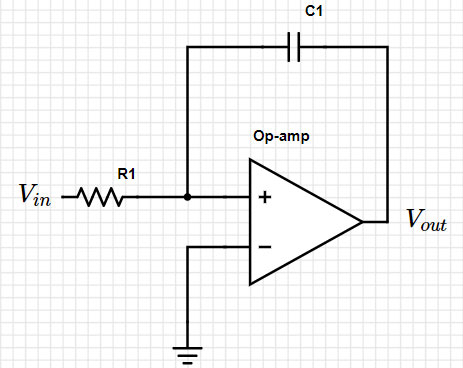 图 1:简单的积分电路。(图片来源:Mustahsin Zarif)
图 1:简单的积分电路。(图片来源:Mustahsin Zarif)
进入拉普拉斯 (Laplace) 域,我们可以用以下公式表示电路:
Vout = -(1/s) (1/RC) Vin
拉普拉斯域中的 1/s 实际上对应于 积分!因此,我们得到一个基于运算放大器的积分电路模型。然而,当我们转向现实世界时,系统会一直受到某种形式的随机噪声污染。
我们暂将积分电路放一放,来看一个更简单的示例:电压放大电路的输入输出波形可通过如图 2 所示的示波器进行测量。
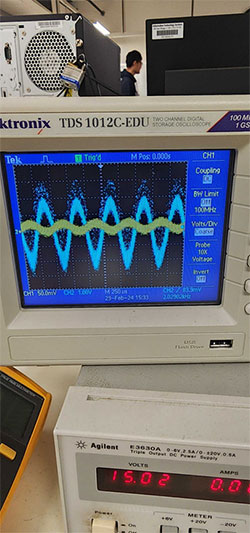 图 2:电压放大器的输入和输出波形。(图片来源:Mustahsin Zarif)
图 2:电压放大器的输入和输出波形。(图片来源:Mustahsin Zarif)
在可见正弦波上叠加的随机噪声有多种原因造成,例如因电路在面包上搭建而产生的电气连接不良等问题。这种噪声同样会干扰积分器的波形,我们将在本信号处理系列后续的博客中对此进行探讨。然而,我们经常考虑的是如何将随机干扰最小化。
滤波技术
工程师喜欢采用滤波技术来克服这些难题。滤波技术可以分为 1) 有限脉冲响应 (FIR) 滤波器或 2) 无限脉冲响应 (IIR) 滤波器。
FIR 滤波器之所以如此命名,是因为任何时候的输出仅取决于当前和先前的输入值值,而不取决于之前的输出值。因此,这种滤波器具有非递归结构,没有反馈,可按照公式 1 建模。
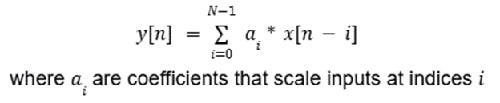 公式 1:FIR 滤波器示例公式。(图片来源:Mustahsin Zarif)
公式 1:FIR 滤波器示例公式。(图片来源:Mustahsin Zarif)
积分器电路就如一个 FIR 滤波器,因为其输出仅取决于输入。
另一方面,IIR 滤波器具有反馈,因为任何时候的输出都取决于先前的输出以及当前输入。这种情况下,可按照公式 2 建模。
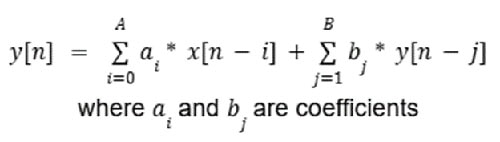 公式 2:IIR 滤波器示例公式。(图片来源:Mustahsin Zarif)
公式 2:IIR 滤波器示例公式。(图片来源:Mustahsin Zarif)
图 3 是 可直观表示 IIR 滤波器的框图,显示了输入和输出如何延迟 (z-i, z-j)、缩放 (ai, bj) 以及相加后获得出当前输出。通过改变这些值,我们可以实现不同类型的滤波器。
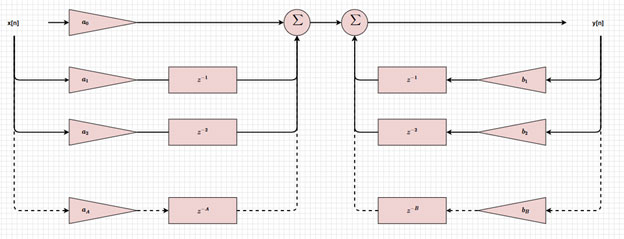 图 3:IIR 滤波器框图。(图片来源:Mustahsin Zarif)
图 3:IIR 滤波器框图。(图片来源:Mustahsin Zarif)
如果我们想要一个无反馈的 FIR 滤波器框图,y[n] 就只是第一次求和的结果(图 4)。
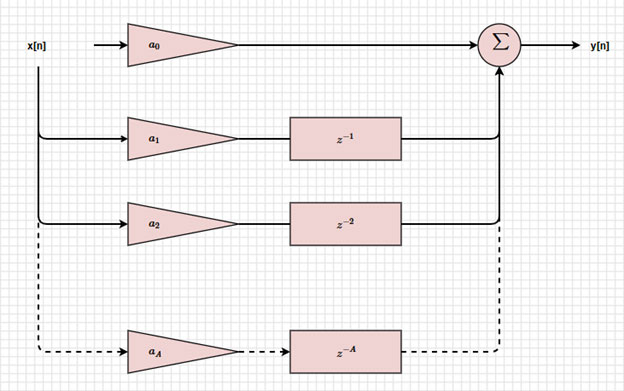 图 4:FIR 滤波器框图。(图片来源:Mustahsin Zarif)
图 4:FIR 滤波器框图。(图片来源:Mustahsin Zarif)
现在,我们已经掌握了 FIR 和 IIR 滤波器的基础知识,接下来用一个例子来说明我们所学到的知识:移动平均滤波器。
移动平均线的工作方式是求出当前输入和一定数量先前输入的平均值(公式 3)。
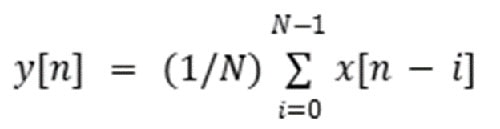 公式3:移动平均公式。(图片来源:Mustahsin Zarif)
公式3:移动平均公式。(图片来源:Mustahsin Zarif)
其中 N= 窗口大小/影响输出结果的样本数
由此看出,这是一个 FIR 滤波器,因为等式右侧没有 y 项。
不过,我们可以巧妙地重组方程,来构造一个 IIR 滤波器。请考虑以下情况:
令 N=5,则
y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5,
且 y[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5
y[6]=(x[6]+y[5]-x[1])/5
因此,当前输出目前取决于之前的输出(y[6] 取决于 y[5])!
更普遍地来说,
y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N
其中 N = 窗口大小
该滤波器在平滑时域信号方面效果奇佳,如图 5 所示,我使用 python 对窗口大小 N = 11 进行了模拟。
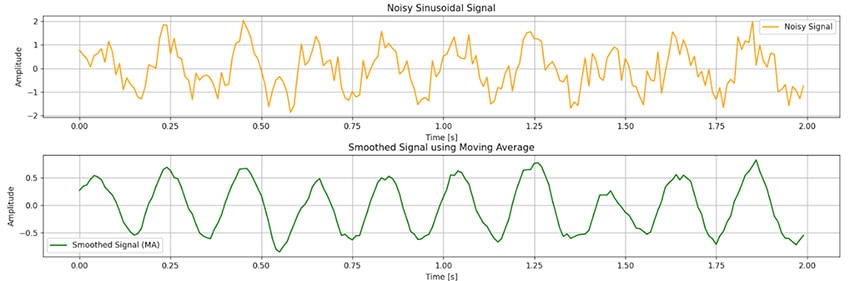 图 5:使用 Python 模拟移动滤波器。(图片来源:Mustahsin Zarif)
图 5:使用 Python 模拟移动滤波器。(图片来源:Mustahsin Zarif)
移动滤波器的 Python 模拟代码:
Copyimport numpy as np
import matplotlib.pyplot as plt
# Parameters for the sinusoidal wave
frequency = 5 # in Hertz
sampling_rate = 100 # Sampling rate in samples per second
duration = 2 # in seconds
# Generate time axis
t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)
# Generate a clean sinusoidal signal
clean_signal = np.sin(2 np.pi frequency * t)
# Add random, white (Gaussian) noise to the signal
noise_amplitude = 0.5
noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)
def moving_average(signal, window_size):
window = np.ones(window_size) / window_size
return np.convolve(signal, window, mode='same')
# Apply moving average to the noisy signal
window_size = 11
smoothed_signal_ma = moving_average(noisy_signal, window_size)
# Plot the noisy and smoothed signals
plt.figure(figsize=(12, 9))
plt.subplot(2, 1, 1)
plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')
plt.title('Noisy Sinusoidal Signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.grid(True)
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')
plt.title('Smoothed Signal using Moving Average')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
结束语
本博客的开头介绍了现实世界中噪音是如何破坏数据的。尽管无法获得数学方程定义的理想响应,但我们可以通过过滤掉所采集数据中的不良特性,使其尽可能接近理想响应。有多种方法可以实现这一点,并且也有多种我们想要实现这一点的场景。虽然我们以移动平均滤波器的模拟响应结束了本篇博客,但在下一篇博客中,我们将研究指数移动平均滤波器如何平滑嘈杂的惯性测量单元 (IMU) 数据!

Have questions or comments? Continue the conversation on TechForum, Digi-Key's online community and technical resource.
Visit TechForum