抗混叠低通滤波器基础知识（及其需要与 ADC 匹配的原因）

无论基本采样数据采集系统无论是用于物联网、智能家居还是工业控制，如果不采取保护措施，都将因混叠而导致不准确问题，因为当模拟输入采样不足而产生杂散信号时，就会发生混叠。混叠将频率高于奈奎斯特频率（采样频率的一半）的信号分量叠回基带频谱，使它们无法与所需信号分离，从而导致误差。另外，高于奈奎斯特频率的噪声也会向下混合至基带，从而降低所需基带信号的信噪比 (SNR)。

若要防止混叠，解决方案是对输入信号进行带宽限制，即将所有输入信号分量限制在模数转换器 (ADC) 采样频率的一半以下。模拟低通滤波器也称为抗混叠滤波器，可用来实现带宽限制。在对带宽进行限制时，滤波器不能增加信号失真、噪声或幅度的频率差异。抗混叠低通滤波器设计必须为快速滚降提供足够的阻带衰减，以降低大幅高于奈奎斯特频率的信号幅度。

本文讨论了抗混叠低通滤波器的设计准则，以及应将它们与 ADC 的规格仔细匹配的原因和方法。然后，文章将展示如何使用 Analog Devices 的示例器件，通过有源或开关电容滤波器元件来实现这些滤波器。

何为混叠？

当系统进行数据采集时，采样率不足就会发生混叠。如果信号包含任何高于奈奎斯特频率的频率，就会与转换器采样器中的采样频率混合，并映射到低于奈奎斯特频率的频率，从而导致不同的信号在采样过程中发生混合且彼此无法区分（即，互相混叠）（图 1）。

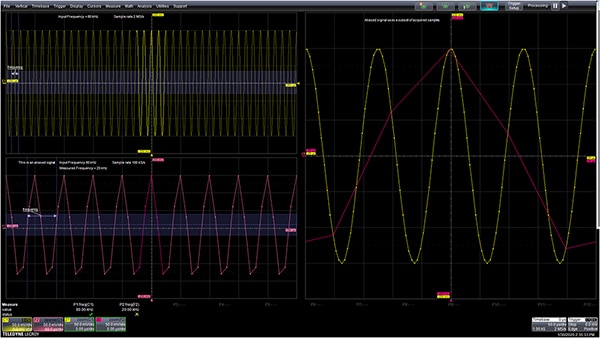图 1：混叠示例。以 2 兆样本/秒采样（左上方）的 80 千赫 (kHz) 正弦波没有混叠现象。而将采样率降至 100 千样本/秒（左下方）时，信号被解释成具有 20 kHz 的频率。在放大视图（右侧）中，正确采样的信号和混叠信号发生了重叠。该迹线上的点显示了样本位置。 请注意，混叠信号使用了正确采样数据的子集。（图片来源：Digi-Key Electronics）

左上方网格中显示的信号是 80 kHz 正弦波，采样率为 2 兆样本/秒 (MS/s)。在 2 MS/s 时，奈奎斯特频率为 1 兆赫 (MHz)；该信号远低于此频率。左下方网格显示了采样率降至 100 千样本/秒 (kS/s) 时发生的情况。此时，奈奎斯特频率为 50 kHz，而 80 kHz 正弦波频率高于奈奎斯特频率，因而发生混叠。

在图像右侧，正确采样和混叠的信号被水平扩展和重叠，其中点表示实际样本。请注意，混叠信号包含以 2 MS/s 采样的信号样本子集。采样是一种混合操作，且该操作的输出由输入信号的和与差以及采样频率组成。

在 100 kS/s 的采样率和 80 kHz 的信号频率下，差频为 20 kHz。两种情况的频率测量值都显示在网格下方。参数读数 P1 读取正确采样信号的频率为 80 kHz，而混叠信号的频率为 20 kHz。

设计抗混叠低通滤波器

在设计抗混叠滤波器时，第一步是确定采集系统所需的带宽。这可确定低通滤波器的截止频率。滤波器截止频率通常设置为 -3 分贝 (dB) 或半功率点。在该频率下，滤波信号的幅度下降至 DC 处幅度的 0.707。如果采集系统设计要求较平坦的频率响应，则可以使用较低的衰减值（例如 -1 dB）来定义截止频率。截止频率幅度越高，抗混叠滤波器频率响应的滚降就越重要。

在确定采集系统的带宽后，即可设置采样率。理论上的最低采样频率是采集系统带宽的两倍。然而，这个理论上的限值在实践中并不是一个很好的采样频率，因为可实现的抗混叠滤波器不可能像完美的理论滤波器那样，硬生生地衰减高于截止频率的信号。这意味着采样率应该更高。这里需要权衡的是，存储器需求会随着采样频率提高而增加。在存储器昂贵的时代，这使得采样率尽可能接近奈奎斯特频率，通常是介于输入带宽的 2.5 到 4 倍之间。而存储器成本的降低放松了此要求，因此采样率可以更高；带宽的五到十倍也并非闻所未闻。

考虑设计一种需要 100 kHz 采集带宽的超声传感器。采样率可以是 500 kHz 至 1 MHz。

现在可以选择 ADC。对于我们的示例，可以选择采样率为 1 MS/s 的 12 位逐次逼近转换器，例如 Analog Devices 的 LTC2365ITS8#TRMPB。其 12 位分辨率可提供 72 dB 的理论动态范围。该 ADC 具有出色的动态性能，包括 -72 dB 的信纳比 (SINAD) 规格和 -73 dB 的 SNR，两者的采样频率均为 1 MS/s（图 2）。

图 2：Analog Devices 的 LTC2365ITS8#TRMPB 12 位逐次逼近 ADC 的框图和 SINAD 性能。（图片来源：Analog Devices）

以 1 MS/s 的采样率运行时，奈奎斯特频率为 500 kHz。100 kHz 低通滤波器的输出必须具有阻带衰减，以使高于奈奎斯特的信号分量下降至 ADC 本底噪声。在本例中，对于高于 500 kHz 的频率，此值大于 -73 dB。

选择滤波器类型

低通滤波器有许多可能的类型或配置。最常用的是巴特沃斯、切比雪夫和贝塞尔滤波器。这些滤波器的频率响应不同，并根据应用提供一些关键的差异因素（图 3）。

图 3：巴特沃斯（灰色）、切比雪夫（蓝色）和贝塞尔（橙色）滤波器的频率响应比较。滤波器的类型区别在于通带平坦性、相位延迟和过渡区的坡度。（图片来源：Digi-Key Electronics）

所示的三种滤波器响应都有各自的具体特点。例如，巴特沃斯滤波器具有最平坦的幅度响应。这意味着，该滤波器在通带频率范围内提供最平坦的增益响应，并在过渡区具有适度的滚降。

贝塞尔滤波器提供统一的时间延迟，以实现恒定的群延迟。这意味着，该滤波器具有随频率变化的线性相位响应和优异的脉冲输入瞬态响应。这种优异的相位响应是以通带的平坦度和通带以外的初始滚降衰减较慢为代价的。

切比雪夫滤波器设计成在过渡区呈现出更陡峭的滚降，但在通带中具有更多的纹波。若设计采用这种滤波器类型，则通常会基于特定的最大纹波。例如，如果截止频率幅度限制为 -1 dB，则纹波规格通常将设置为最大 1 dB。

这些滤波器在时域中对脉冲的响应有助于理解如何选择适当的滤波器类型（图 4）。

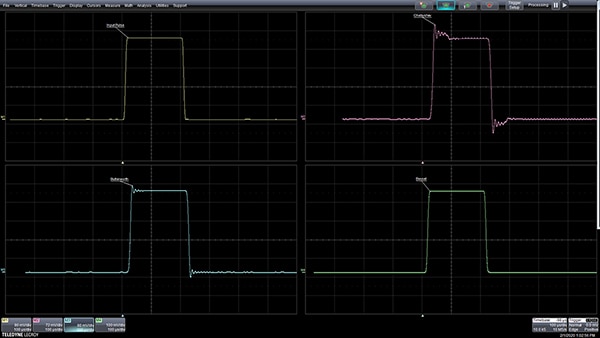图 4：滤波器对输入脉冲的响应（左上角）在切比雪夫（右上角）、巴特沃斯（左下角）和贝塞尔（右下角）滤波器类型中表现出时域脉冲响应差异。（图片来源：Digi-Key Electronics）

贝塞尔滤波器具有线性相位频率响应，能够使脉冲以最小的失真通过，但既没有巴特沃斯滤波器的幅度平坦度，也没有切比雪夫滤波器的锐截止特性。选择的过滤器类型取决于应用：

• 如果幅度精度是最重要的考虑因素，则应选择巴特沃斯滤波器
• 如果所需的采样率接近信号带宽，则切比雪夫滤波器将是首选
• 如果主要考虑脉冲保真度，则贝塞尔滤波器是最佳选择

滤波器阶数

滤波器阶数代表了指滤波器设计的复杂性。该术语与设计中电抗元件（例如电容器）的数量有关。此外，它还代表了滤波器传递函数中的极数。

滤波器的阶数影响过渡区滚降的陡度，进而影响过渡区的宽度。一阶滤波器的滚降为每倍频程 6 dB，或每十倍频程 20 dB。n 阶滤波器的滚降速率为 6×n dB/倍频程或 20×n dB/十倍频程。因此，一个八阶滤波器的滚降率为每倍频程 48 dB 或每十倍频程 160 dB。

以前文所述的超声传感器设计为例，按照 500 kHz 的奈奎斯特频率来算，所有高于 100 kHz 的信号都需要衰减至少 -73 dB。八阶滤波器在 500 kHz 下将信号衰减约 -98 dB（图 5）。六阶滤波器在 500 kHz 下将带外信号衰减约 -83 dB。 因此，对于我们的示例，使用六阶滤波器就足够了，但是使用八阶滤波器可以提供更低的带外信号幅度。如果成本相同，则应选择八阶滤波器。稍后在讨论元器件时，将对这种权衡进行更多讨论。

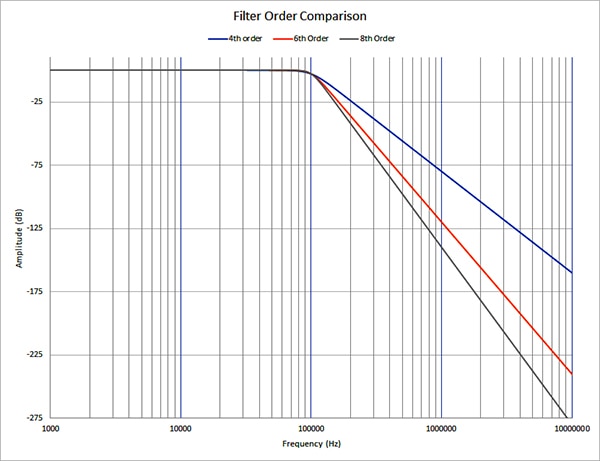图 5：比较四阶（蓝色）、六阶（橙色）和八阶（灰色）滤波器响应的滚降。（图片来源：Digi-Key Electronics）

滤波器的阶数可通过级联多个滤波器来增加。例如，两个二阶低通滤波器可以级联在一起，以构成一个四阶低通滤波器，依此类推。多个有源滤波器的级联代价是，功耗、成本和尺寸都会增加。

六阶或八阶滤波器的选择还取决于所选滤波器元器件的可配置性。滤波器 IC 若配置为四个二阶滤波器，则可以实现一个六阶滤波器，但若滤波器 IC 配置为双四阶滤波器，则只能实现一个八阶滤波器。

滤波器组件

抗混叠滤波器若要用于声频和超声频率，则可以使用有源或开关电容滤波器来实现。通常，使用任一滤波器类型的结果非常相似。在使用 16 或更高位超高分辨率 ADC 的应用中，由于出现噪声的可能性较低，因此首选有源滤波器。开关电容滤波器需要时钟信号，因此出现噪声的可能性较高，这是由于来自时钟信号的串扰导致。

Analog Devices 的 LTC1563 系列提供 4 极或四阶有源滤波器，它们使用单个电阻器来控制截止频率。该系列提供巴特沃斯或贝塞尔型滤波器配置。LTC1563-2 是一款 4 极巴特沃斯配置的滤波器元器件，最大截止频率为 256 kHz。该滤波器 IC 可以通过级联方式实现八阶低通响应（图 6）。

图 6：使用两个 Analog Devices 的 LTC1563-2 器件实现的一个八阶 20 kHz 巴特沃斯滤波器。（图片来源：Analog Devices）

如果应用需要可变的截止频率，则 Analog Devices 的 LTC1564IG#TRPBF 是一个不错的选择。该八阶低通滤波器使用 4 位控制总线以数字方式控制带宽，可在 10 kHz 到 150 kHz 的范围内以 10 kHz 步幅变动截止频率。此外，增益也可按数字方式进行编程。该滤波器具有 122 dB 的动态范围，适用于 16 至 20 位分辨率的采集系统（图 7）。

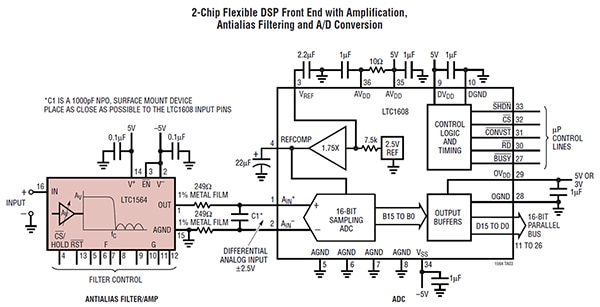图 7：仅使用两个 IC 的 16 位 500 kS/s 采集系统。LTC1564IG#TRPBF 提供高达 150 kHz 的可变带宽和高达 24 dB 的增益。（图片来源：Analog Devices）

此外，可变截止频率设计也可以通过开关电容滤波器来实现。Analog Devices 的 LTC1068-25IG#PBF 是一款通用开关电容器八阶低通滤波器，最大截止频率为 200 kHz。该 IC 由四个二阶滤波器构件组成，可以通过级联方式创建八阶低通滤波器（图 8）。

图 8：使用 LTC1068-25IG#PBF 开关电容滤波器的八阶低通滤波器。截止频率使用开关时钟来设置，等于开关时钟频率除以 32。（图片来源：Analog Devices）

通用有源滤波器 IC 也可以用于抗混叠。它们需要更多的元件来设置滤波器特性。Analog Devices 的 LTC1562-2 是一款低噪声/低失真的四二阶滤波器，可以配置为具有低通、高通或带通响应的巴特沃斯、切比雪夫、椭圆或等纹波延迟响应滤波器。截止频率为 20 至 300 kHz，可使用电阻值进行编程。通过三个电阻器可设定中心频率、增益和 Q 值。该四二阶滤波器的设计可配置为产生二阶、四阶、六阶或八阶滤波器。

总结

数据采集系统需要使用抗混叠低通滤波器，以确保可以正确地重建所有目标采样信号。所需的滤波器特征取决于与之配对的 ADC 的带宽、幅度分辨率和采样率。如上所述，有多种设计选项可用于实现低通滤波器，包括有源、数字可控和开关电容器件。